
Statistical hypothesis testing is a fundamental tool used in various fields, from science and medicine to social research and business. It allows us to draw conclusions about populations based on data collected from samples. At the heart of this process lie two key concepts: the null hypothesis and the alternative hypothesis,hypothesis and null hypothesis. This article will delve into these concepts, explaining their roles in hypothesis testing and how they work together to guide our understanding of data.this article gives you a clear idea of alternative and null hypothesis in general.this basics of fundamental of research can be read and understood with Amrita AHEAD.
A hypothesis is a proposed explanation for a phenomenon that can be tested. It’s like an educated guess that scientists use to figure out how things work. It should be based on some evidence and be specific enough to be tested through experiments or research.
Observation: Students who get a good night’s sleep tend to perform better on tests.
Hypothesis: Students who sleep for 8 hours or more the night before a test will score higher on average than students who sleep for less than 8 hours.
This hypothesis is testable because we can track students’ sleep habits and then compare them to their test scores. It’s based on some evidence – we know sleep is important for cognitive function. The hypothesis is also specific – it defines a clear amount of sleep (8 hours) and predicts an outcome (higher scores).
Examining the Hypothesis:Here’s the diagrammatic representation of how we could examine hypothesis:
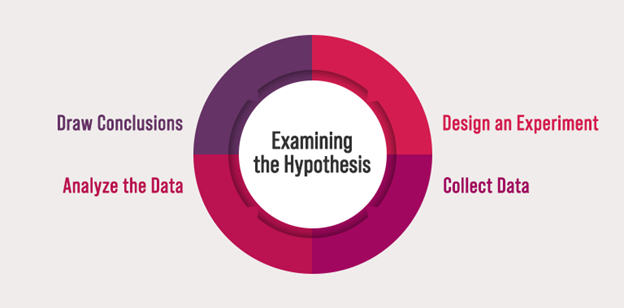
How to Examine a Hypothesis
By following these steps, researchers can refine their understanding of the relationship between sleep and academic performance probing deep into alternative and null hypothesis.
Hypothesis testing is a scientific method used in statistics to evaluate ideas or claims about a population. It involves a structured approach to analyze data and see if it supports a particular notion. Here’s a breakdown of the process:
Formulating the Hypotheses:
In essence, hypothesis testing provides a framework to weigh evidence against a starting assumption (null hypothesis) and see if it holds up. It’s a crucial tool in various fields like medicine, social science, and marketing to make data-driven decisions and advance our understanding of the world.
A hypothesis, in the context of statistics, is a tentative statement about a population parameter. It represents a prediction or an educated guess about the relationship between variables. The null hypothesis (denoted by H₀), specifically, is a statement that claims no significant difference exists between the groups being compared or that there is no effect of a particular treatment or intervention.
Here are some key points to remember about the null hypothesis:
For example, a researcher might hypothesize that a new fertilizer will increase crop yield. The null hypothesis in this scenario would be that there is no difference in yield between crops treated with the new fertilizer and those with a standard fertilizer.
The term “test hypothesis” is sometimes used interchangeably with the null hypothesis. However, it can have a broader meaning. In some contexts, it refers to the entire hypothesis testing framework, encompassing both the null hypothesis and the alternative hypothesis (explained later).
Here, we’ll focus on the null hypothesis as the most common interpretation of “test hypothesis.”
The zero hypothesis (H₀) is another term for the null hypothesis. It emphasizes the idea of “no difference” or “no effect” that the null hypothesis proposes.
The alternative hypothesis (denoted by H₁), on the other hand, is the opposite of the null hypothesis. It represents the predicted effect or the directional statement about the relationship between variables. It’s what we believe to be true if the null hypothesis is false.
Here are some key points about the alternative hypothesis:
In our crop yield example, the alternative hypothesis could be that the new fertilizer will increase crop yield (one-tailed) or that it will affect yield in some way (two-tailed, positive or negative).
The key difference betweenhypothesis and alternative hypothesis lies in their specificity. A hypothesis can be a broad statement about a relationship between variables, while the alternative hypothesis is a more precise prediction based on the researcher’s specific question. Additionally, the null hypothesis is a specific type of hypothesis that proposes “no difference” or “no effect.”Here is table showing the major differences between hypothesis and alternative hypothesis.
|
Feature |
Hypothesis (H₀) |
Alternative Hypothesis (H₁) |
|
Definition |
A statement that proposes no significant difference between variables or claims there is no effect of a treatment. |
A statement that proposes there is a significant difference between variables or claims there is an effect of a treatment. |
|
Viewpoint |
Represents the default or null position. |
Represents the opposite of the null hypothesis and what the researcher is trying to prove. |
|
Expectation |
We expect no change or relationship to be observed. |
We expect to observe a change or relationship. |
|
Outcome When Accepted |
No further investigation is typically needed. |
The null hypothesis is rejected, and the alternative hypothesis is tentatively accepted. |
|
Example (Sleep & Grades) |
Students who get any amount of sleep will score the same on average as those who don’t get any sleep. |
Students who sleep for 8 hours or more the night before a test will score higher on average than students who sleep for less than 8 hours. |
Here is a table for Null Hypothesis vs. Alternative Hypothesis
|
Feature |
Null Hypothesis (H0) |
Alternative Hypothesis (Ha) |
|
Function |
Represents the “no effect” scenario |
Represents the expected effect |
|
Prediction |
There is no significant relationship or difference between variables. |
There is a significant relationship or difference between variables. |
|
Direction |
Unspecified (no direction of change) |
Can be one-tailed (predicts a specific direction of change) or two-tailed (predicts any difference) |
|
Burden of Proof |
Not rejected (considered true unless evidence suggests otherwise) |
Must be proven with statistical evidence |
|
Wording |
Often phrased with “no difference” or “no effect” |
More specific, stating the expected change or relationship |
|
Example (Simple) |
* Average exam scores for both groups are equal. |
* Students who took the practice test will score higher. |
|
Example (Directional) |
* Exercise has no impact on weight loss. |
* A weight loss program combined with exercise will lead to greater weight loss compared to diet alone. |
|
Real-World Application |
Helps researchers avoid bias by starting with a neutral assumption. |
Guides the research by outlining the effect being investigated. |
Hypothesis testing uses null (H₀) and alternative (H₁) hypotheses to investigate relationships between variables. We aim to reject the null hypothesis (no difference) in favor of the alternative (a difference). However, interpreting results requires considering statistical significance, effect size, and study limitations. Understanding these concepts allows researchers to make data-driven decisions.Now that you have understood what exactly is alternative and null hypothesis you can call it a day.
You May Like